How to Optimally Sample Imbalanced Data: A Practical Guide

Visual Overview

Introduction

Dealing with imbalanced datasets is one of the most common challenges in machine learning. When one class significantly outnumbers others, models often become biased toward the majority class, leading to poor performance on minority classes. This issue is especially critical in domains like fraud detection, medical diagnostics, and rare event prediction.

This guide outlines a 4-step process for optimal sampling of imbalanced data, leveraging a pilot model and data scoring to create balanced training sets while maintaining unbiased model estimates. Let’s dive into the methodology step by step.

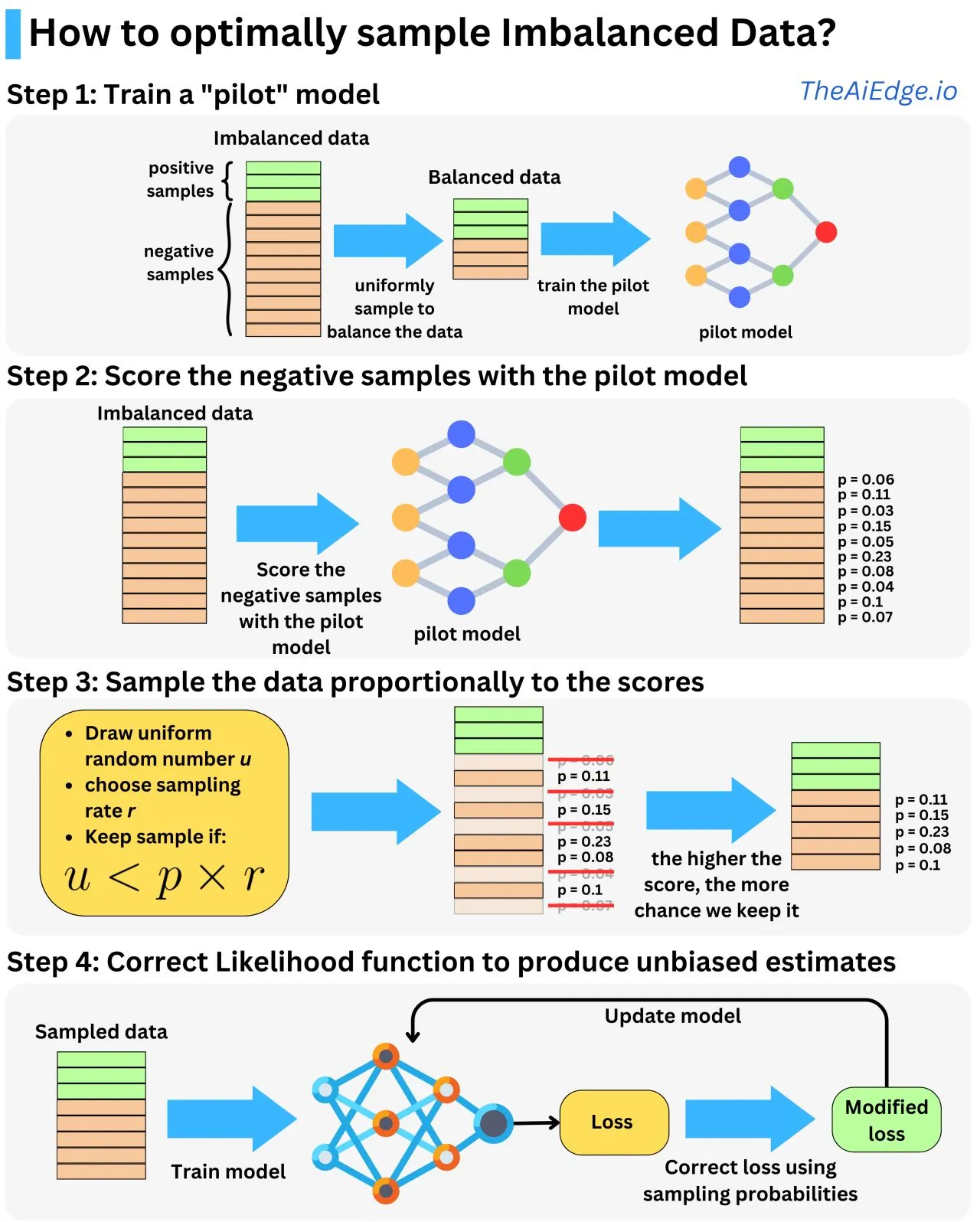
Step 1: Train a “Pilot” Model

Overview

The first step involves training a pilot model on a balanced version of your imbalanced dataset. To achieve this:

Uniformly sample the majority and minority classes to create a balanced dataset.
Train a preliminary model (pilot model) on this balanced dataset.

Why This Is Important

The pilot model acts as a preliminary predictor, which will later be used to estimate the likelihood of samples belonging to the minority class. This lays the foundation for scoring and sampling the imbalanced data more effectively in subsequent steps.

Step 2: Score the Negative (Majority) Samples with the Pilot Model

Overview

Once the pilot model is trained, use it to score the samples in your imbalanced dataset. Specifically:

Feed the negative (majority class) samples through the pilot model.
Assign scores to these samples based on their likelihood of belonging to the minority class.

Why This Is Important

The assigned scores provide a quantitative measure of how relevant each sample is for improving the model’s understanding of the minority class. This scoring step ensures that not all majority samples are treated equally in the next phase.

Step 3: Sample the Data Proportionally to the Scores

Overview

In this step, you selectively sample data based on the scores computed in Step 2. Follow these steps:

For each sample, draw a uniform random number (u).
Define a sampling rate (r), which controls the proportion of data to retain.
Retain a sample if (u < p × r), where (p) is the sample’s score.

This method ensures that samples with higher scores (closer to the minority class) are more likely to be included in the training set.

Why This Is Important

This approach prioritizes informative majority-class samples while discarding irrelevant ones, creating a dataset that is both representative and efficient for model training.

Step 4: Correct the Likelihood Function for Unbiased Estimates

Overview

After constructing your sampled dataset, train the model on this new data. However, sampling introduces bias, so it’s crucial to adjust the likelihood function to account for the sampling probabilities. This ensures unbiased estimates.

To do this:

Modify the loss function by incorporating the sampling probabilities from Step 3.
Train your final model using the corrected loss function.

Why This Is Important

Correcting the loss ensures that the model does not overfit or skew predictions based on the sampled data. It guarantees that the model generalizes well to the original distribution of the data.

Why This Approach Works

This 4-step methodology optimally handles imbalanced data by:

Reducing Class Imbalance: Ensures the model trains on a balanced dataset.
Prioritizing Informative Samples: Selects the most relevant majority-class samples for training.
Maintaining Unbiased Estimates: Adjusts the likelihood function to reflect the true data distribution.
Enhancing Model Performance: Improves generalization to minority classes without overfitting.

When to Use This Approach

This method is particularly useful when:

The dataset has a high class imbalance (e.g., 1:100 or more).
Minority-class samples are extremely rare and valuable.
Computational resources are limited, and training on the full dataset is infeasible.
Precision on the minority class is a key metric for success.

Conclusion

Handling imbalanced datasets is critical for building robust machine learning models. By training a pilot model, scoring data, sampling proportionally, and correcting the likelihood function, this method provides an efficient, scalable solution for improving performance on minority classes.

Adopting this approach can help unlock better predictions in applications where every minority-class prediction counts, such as fraud detection, rare disease diagnosis, and anomaly detection.