Cross-Validation Techniques for Financial Time Series Forecasting
FREEFinancial time series forecasting is an important task in the financial industry, as it allows organizations to make better investment decisions and manage risk more effectively. One of the key challenges in time series forecasting is ensuring the accuracy and robustness of the predictions. Cross-validation is a widely used technique that can help to address this challenge. Here I will explain the importance of cross-validation in financial time series forecasting and different techniques that can be used.
Cross-Validation
Cross-validation is a statistical method that is used to evaluate the performance of machine learning models. It involves dividing the dataset into subsets, called folds, and training the model on different subsets while testing it on the remaining ones. This allows for a more robust evaluation of the model's performance, as it takes into account the variability of the data and reduces the risk of overfitting.
Let’s deep dive into some cross-validation techniques.
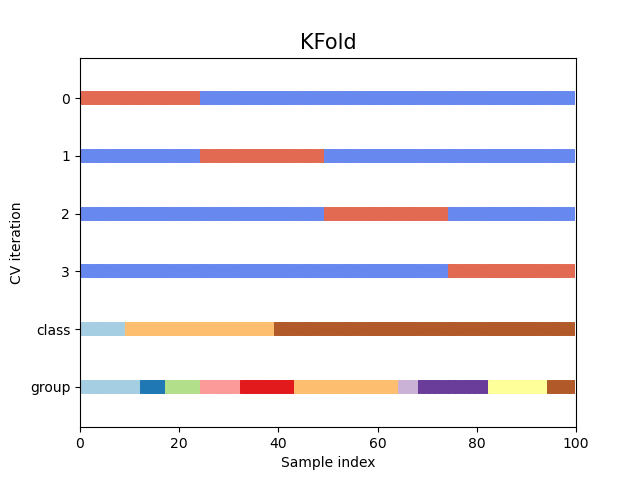
K-Fold Cross-Validation
This technique involves dividing the data into k folds and training the model k times, each time using a different fold as the test set. It's a common method, simple to implement and useful for large datasets.
source: https://scikit-learn.org/stable/auto_examples/model_selection/plot_cv_indices.html
Here is an example of code to implement the k-fold cross-validation:
from sklearn.model_selection import KFold
kf = KFold(n_splits=5)
for train_index, test_index in kf.split(financial_data):
X_train, X_test = financial_data[train_index], financial_data[test_index]
y_train, y_test = labels[train_index], labels[test_index]
model.fit(X_train, y_train)
predictions = model.predict(X_test)
# Evaluate the performance
This approach is not so suitable for time-series data. Some drawbacks:
- Temporal dependence: Time series data exhibits temporal dependence, meaning that the order of the data points matters. When using k-fold cross-validation on time series data, there is a risk of introducing data leakage across folds, which can lead to overly optimistic performance estimates. This occurs because the temporal order of the data is not preserved in k-fold cross-validation. The model may be trained on future data points that are used in the validation set, leading to overfitting.
- Inability to account for time-varying patterns: Time series data often exhibits time-varying patterns such as trends, seasonality, and autocorrelation. These patterns can change over time, making it difficult to evaluate the performance of the model using k-fold cross-validation. This is because k-fold cross-validation assumes that the data is stationary, and the same patterns are present in all folds.
- Difficulty in determining the optimal number of folds: In k-fold cross-validation, the value of k is typically set based on some heuristics, such as using 5 or 10 folds. However, it may not be clear what value of k is optimal for time series data, and using an inappropriate value of k can lead to biased performance estimates.
- Difficulty in handling irregularly spaced data: Time series data can be irregularly spaced, with missing or unevenly spaced data points. K-fold cross-validation assumes that the data is regularly spaced, and it may not be able to handle missing data or irregularly spaced data points.
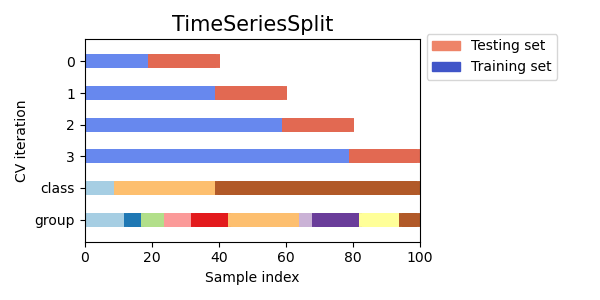
Time-Series Split Cross-Validation
This technique is specifically designed for time series data and involves dividing the data into train and test sets based on a fixed time period. This method takes into account the temporal dependencies of the data and is useful for financial time series forecasting.
source: https://scikit-learn.org/stable/auto_examples/model_selection/plot_cv_indices.html
In python:
from sklearn.model_selection import TimeSeriesSplit
tscv = TimeSeriesSplit(n_splits=5)
for train_index, test_index in tscv.split(financial_data):
X_train, X_test = financial_data[train_index], financial_data[test_index]
y_train, y_test = labels[train_index], labels[test_index]
model.fit(X_train, y_train)
predictions = model.predict(X_test)
# Evaluate the performance
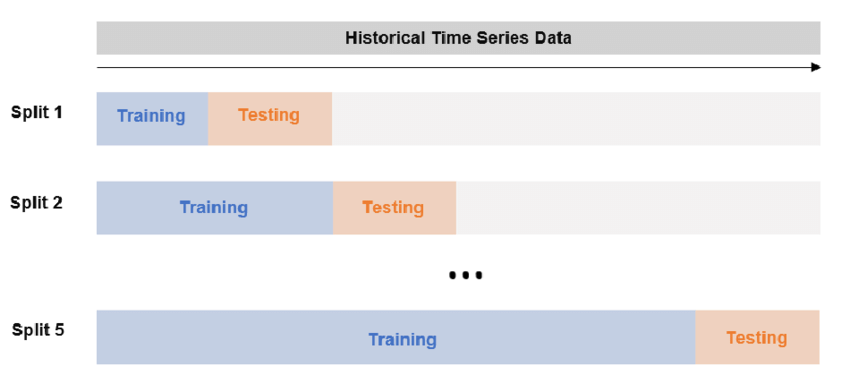
Expanding Window Cross-Validation
The basic idea behind Expanding Window Cross-Validation is to use a sliding window to partition the time series data into a series of training and testing sets. The size of the window increases over time, so that the model is trained on an expanding set of past data and tested on the most recent data.
It's useful when working with very large datasets or when there is a temporal dependency in the data.
In financial time series analysis, this approach is often used to evaluate the performance of trading strategies over time. For example, suppose you have a trading strategy that involves making predictions about the future direction of a stock price based on past price data and other relevant features. You could use Expanding Window Cross-Validation to evaluate how well the trading strategy performs over time, by training the model on past data and testing it on future data.
from sklearn.model_selection import TimeSeriesSplit
<h1 id="define-the-number-of-splits-for-expanding-window-cross-validation">Define the number of splits for expanding window cross-validation</h1>
n_splits = 5
<h1 id="initialize-the-expanding-window-cross-validation-object">Initialize the expanding window cross-validation object</h1>
tscv = TimeSeriesSplit(n_splits=n_splits)
<h1 id="iterate-over-the-splits-and-fit-the-model">Iterate over the splits and fit the model</h1>
for train_index, test_index in tscv.split(data):
# Get the training and testing data for this split
X_train, X_test = data[:train_index[-1]+1], data[train_index[-1]+1:test_index[-1]+1]
y_train, y_test = np.arange(train_index[-1]+1), np.arange(test_index[-1]+1-train_index[-1]-1)
model.fit(X_train, y_train)
predictions = model.predict(X_test)
# Evaluate the performance
Conclusion
It's important to note that the choice of cross-validation technique will depend on the specific use case and the data you are working with. Now you know some basic technique for handling the financial time-series cross-validation







